牛油貓的筆記: 11/05/20

簡介
強化學習 (Reinforcement Learning) 是一種透過嘗試做不同決策，然後根據所獲取的奬勵 (Rewards) 或懲罰 (Punishment)，找出最佳解 (Optimized Solution) 的算法。由於它採用分數奬勵的形式訓練，所以它特別適合玩迷宮、小遊戲、甚至訓練機器人走路這類「未必有絕對答案，只需完成目的」的應用。

強化學習與監督學習 (Supervised Learning) 有所不同的是：監督學習需要集齊不同迷宮的最佳解，然後讓系統在訓練模式中找出 hidden pattern。相反，強化學習並不需要有最佳解的數據庫：系統只需透過選擇性地嘗試，然後採取最低風險（最高回報）的做法，最後就能找出接近最佳解。

以下會利用 Q-Learning 作為例子，講解算式，最後會用一個程式例子演示。

使用「類 Markov Matrix」表示奬勵積分
以下內容，節錄自 A Painless Q-Learning Tutorial [1]。

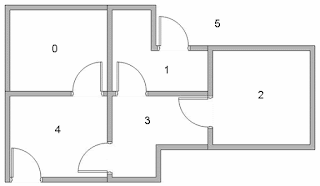
假設有五間房，我需要設計一個使用 Q-Learning 離開房間的程式的話，我可以假設每一間房為一個 state （state 0 - 4 共五個 state），而「房間外」則為「State 5」，所以一共有六個 state：

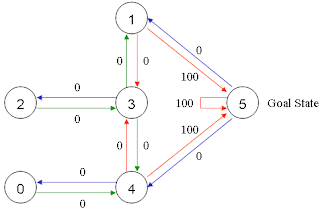
然後，為了鼓勵人離開房間，每當離開所有房間（也就是去到 State 5），我都會奬勵它 100 分，其餘行動則獲得 0 分：

最後，我們可以用矩陣去表達這個 Markov Decision Chain，當中不存在的事件，我們之後會忽略掉不計。為了整齊，這裏暫時會用 -1 代表：

例子：
如果我在 State 1，想跳去 State 5，將會得到 100 分奬勵。
如果我在 State 2，想跳去 State 3，將會獲得 0 分奬勵。
如果我在 State 4，想跳去 State 1，我們會忽略這個情況，因為並不合法。

簡化版 Q-Learning 算式
定好了 Reward Table，就可以開始 Q-Table 演算。Q-Table 是一個儲存經驗值的矩陣，經過一輪運算，這個 Table 中的數值，將會幫助系統找出最佳解。

以下例子，會用簡化版 (learning rate = 1) 去講解：
（正常版的數式在 Wikipedia 中有提及，但由於比較複雜，所以不在此詳述）

運算步驟：

首先選一個起點（例子：State 2）和一個終點（離開房間 = State 5）
重覆以下步驟，直至到達終點為止：

用 Q-Table Equation 更新 Q-Table:

任意取下一點 S，獲取奬勵 R，
基於 S 點，找出 Q-Table 中最大數值的點（若同樣則任意選一點）

將 S 變成現時點，繼續重覆上一步

例子（假設 gamma 為 0.8）：

初始值 Q-Table 全為零。

選取起點 State 1，然後從 S=(3,5) 中任意選一點， S=5，
基於 S=5，可以去 (1,4,5) 三點，但 Q-Table 中去三點 (Q(5,1), Q(5,4), Q(5,5)) 均為零，
所以任意選 5，並更新 Q Table 值：Q(1,5) = R(1,5) + 0.8*0 = 100
最後，將 S=5 變成現時點，但由於現時點＝終點，所以計算結束。

選取起點 State 3，然後從 S=(1,2,4) 中任意選一點，S=1，
基於 S=1，可以去 (3,5) 兩點，而 Q-Table 中 Q(1,3)=0, Q(1,5)=100，因選最大，所以選 5。
然後更新 Q Table 值：Q(3,1) = R(3,1) + 0.8*100 = 0+80 = 80
最後，將 S=5 變成現時點，但由於現時點＝終點，所以計算結束。

選取起點 State 0，然後從 S=(4) 中任意選一點，S=4，
基於 S=4，可以去 (3,5) 兩點，而 Q-Table 中 Q(4,3) 和 Q(4,5) 均為零，
所以任意選 3，並更新 Q Table 值： Q(0,4) = R(0,4) + 0.8*0 = 0，
最後，將 S=4 變成現時點，繼續運算：

選取起點 State 4，然後從 S=(3,5) 中任意選一點，S=3，
基於 S=3，可以去 (1,2,4) 三點，而 Q-Table (Q(3,1), Q(3,2), Q(3,4)) 中，
因 Q(3,1)=80 為最大，所以選 1，並更新 Q-Table 值：Q(4,3) = R(4,3) + 0.8*80 = 64，
最後，將 S=1 變成現時點，繼續運算：

選取起點 State 1，然後從 S=(3,5) 中任意選一點， S=5，
基於 S=5，可以去 (1,4,5) 三點，而 Q-Table (Q(5,1), Q(5,4), Q(5,5)) 中，三點均為零，
所以任意選 5，並更新 Q Table 值：Q(1,5) = R(1,5) + 0.8*0 = 100
最後，將 S=5 變成現時點，但由於現時點＝終點，所以計算結束。

經過以上幾輪計算，得出以下 Q-Table 值：
Q(1,5) = 100 / Q(3,1) = 80 / Q(0,4) = 0 / Q(4,3) = 64

若果經過更多輪計算，不同數值將會繼續更新，
但最後，均會大約在以下結果中，開始收歛 (convergence)：