簡介
很多時候,當我們得到一大堆數據,要進行數據分析的時候,我們都會先篩選一些比較重要的變數,然後才把它們放進 Machine Learning 的算法當中,以節省電腦的運算時間。不過,當篩選出來的數據仍然很多,有時候就令人頭痛。到底有沒有方法,可以用一個變數去取代數個相似的變數呢?(例如「氣温」和「季節」很相近,可否結合成一個變數,例如「天氣」來代表呢?)
另一種情況,就是當我們得到一大堆數據,希望用 ML 做分辨系統,我們也會問:到底這個 project 的可行性有多高?數據之間是否存在著一些,可用 2D 或 3D 的圖表展示的規律?
面對這兩種情況,降維 (Dimensionality Reduction) 就能幫助我們達到以上的目的 。這裏的「維度 (Dimension / Dimensionality)」是指變數(例如氣温、季節等)。而降低維度,正正就是指把 N 個變數,變成 K 個變數(當中 N >= K)。是次會以 PCA 算法作為例子,簡介一下到底大致原理是什麼,以及有什麼應用。
Principal Component Analysis (PCA) 的目的
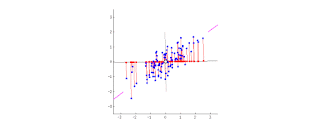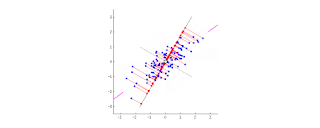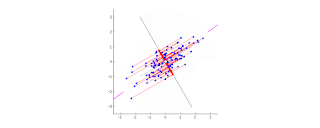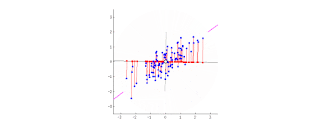
顧名思義,這個算法的目的,就是要找出一大堆數據中最有代表性的 Vector(或者叫 Principal Component)。舉例來說,以下的 2D 例子中有五點,當中最有代表性的 vector 就是 (1/sqrt(2), 1/sqrt(2)),也就是藍色的箭頭:
算法的目的,就是從 2D 平面中,找出那條藍色箭頭,然後,以上五點大約的位置 ,就能以投影的方式,在 1D 的線上表示。正如下圖左下方的例子,原本 x(1) 需要以 2D (x2, x1) 的方法表示,但當找到藍色 vector 之後,就能以 1D,也就是 x(1) = m*(z1) 的方法表示(當中 m 代表長度):
如此類推的話,即使原本變數有非常多個(例如 1600 個),只要使用 PCA 不斷投射,我們就可以將變數縮成數個(例如 2 個),然後用圖表去表示數據分布,如下圖所示,PCA 能找出一大堆國家,在 2D 平面下的分布情況:
PCA 的算法
既然 PCA 這麼實用,我們當然想了解它的原理與算法。不過由於它涉及到找出 eigenvectors 等等一大堆 linear algebra 的概念,以及一大堆數學證明,以下部分,只提到基本概念和步驟。詳細證明方法可以參考 CSDN 的文章。
基本概念:
PCA 的目的,在於找出所有投影平面/線中,可以產生最小總距離的兩支 vectors(正負)。
如下圖所示,世界中有超多的 vector,但我只想要 y=x 的那一支:
基本步驟(取自 Coursera):
- 計算 covariance matrix,sigma = (1/m)*(x(i))*(x(i))T
- 用 SVD 計算 eigenvector of matrix sigma,得出 [U, S, V]
- 抽取 U matrix 中的首 K 行,成為 Ureduced
- 得出 Z = UreducedT * x(i)
PCA 程式演示
由於 Python 中的 scikit 一早已經寫好了 PCA 的算法,我們可以直接使用,參見以下例子:
https://github.com/cmcvista/MLHelloWorld/blob/main/PCADimensionalityReduction.ipynb
---
參考:
[1] - Andrew Ng - Machine Learning Course in Coursera - https://www.coursera.org/learn/machine-learning/lecture/ZYIPa/principal-component-analysis-algorithm
[2] - https://zhuanlan.zhihu.com/p/37777074